What are vectors?

This is not a math tutorial. See Why am I writing about math?

“Most generally, a vector is a list of things. In mutivariable calculus, ’thing’ typically ends up meaning ’number’, but not always.”¹

Operations that can be performed on vectors

Between vectors of equal length:

• addition
• subtraction
• dot product multiplication

Vectors can also be scaled with scalar multiplication.

Vectors versus points

When a vector is a list of numbers, it can be visualized as an arrow in space with its tail at the origin. For example (3, 4):

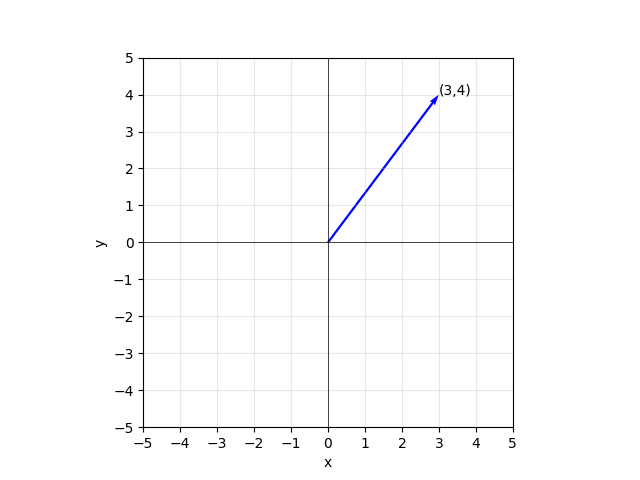
Python code for generating the image.

The same vector (3, 4) can be drawn with its tail at some point other than the origin (0, 0). In the image below, both arrows correspond to the same vector (3, 4), even though they have different origins. The vector (3, 4) represents the same displacement regardless of where it’s drawn from (regardless of what it’s point of origin is considered to be).

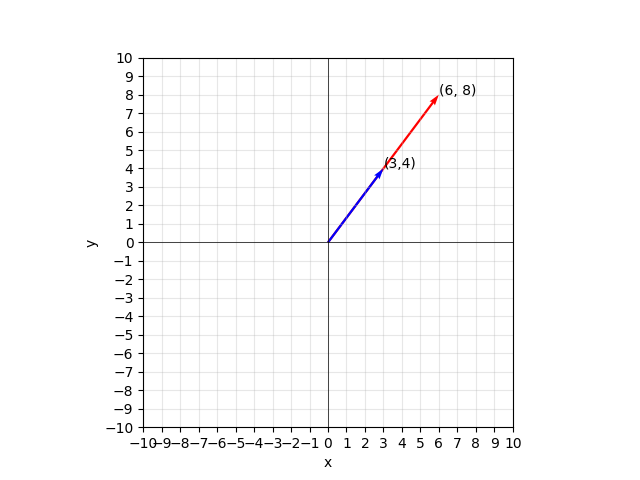
Python code for generating the image

Magnitude and direction

A vector has a magnitude and a direction.

The magnitude, or length, of a vector is the square root of the sum of its squares.

For 2D vectors, the magnitude is the hypotenuse, because a 2D vector can be thought of as the hypotenuse of a triangle.

Considering a single 2D vector, the direction can be expressed as the angle from the positive x-axis. For example, given the vector (3, 4), and remembering SOHCAHTOA (cosine = adjacent / hypotenuse):

The hypotenuse is also the magnitude that was calculated above:

The direction of the vector (3, 4) is the angle of the cosine of the point (3, 4):

theta = 3/5
angle = np.degrees(np.arccos(theta))
angle = 53.13010235415598

Cosine similarity

Consider the vectors (3, 4) and (6, 8):

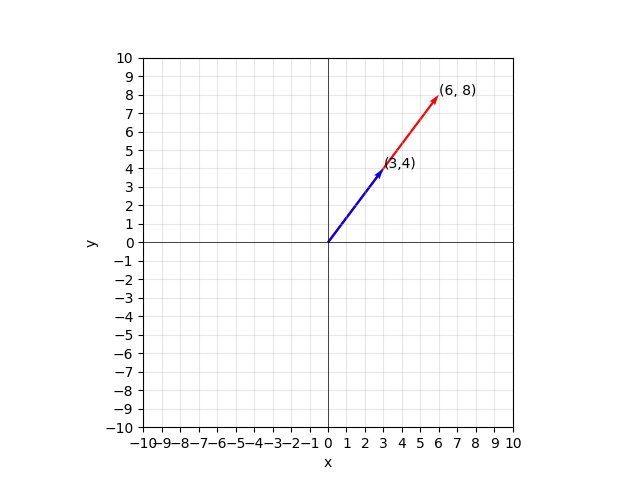
The vector (3, 4) has a magnitude of $\sqrt{3 ^2 + 4^2} = 5$. The vector (6, 8) has a magnitude of $\sqrt{6^2 + 8^2} = 10$

The vectors have different sizes/lengths/magnitudes, but they have the same direction/angle: $\approx 53.13^\circ$.

Cosine similarity, a measure of the similarity between vectors that’s used in semantic search applications, is a measure of the direction of vectors. It completely ignores the magnitude:

That means, the dot product of $A$ and $B$ divided by the product of the magnitudes of $A$ and $B$.

The (general) meaning of the dot product of two vectors

• positive dot product: the vectors point in generally the same direction
• zero dot product: the vectors are perpendicular (orthogonal, completely unrelated directions)
• negative dot product: the vectors point in opposite directions

Dividing by the magnitudes normalizes away the length information

Given: (3, 4) and (6, 8):

Dividing by the product of the magnitudes constrains (normalizes) the result to $[-1, 1]$.

The meaning of direction and magnitude in terms of semantic analysis of text

Tentatively, direction is a measure of “what is this text talking about” and magnitude is a measure of how emphatic the text is, or how much text there is. (That seems a little too convenient, but also kind of right.)

References

Khan Academy. “Vectors and notation.” Accessed on: January 14, 2026. https://www.khanacademy.org/math/multivariable-calculus/thinking-about-multivariable-function/x786f2022:vectors-and-matrices/a/vectors-and-notation-mvc .