Creating a unit circle graph with Processing

January 21, 2026

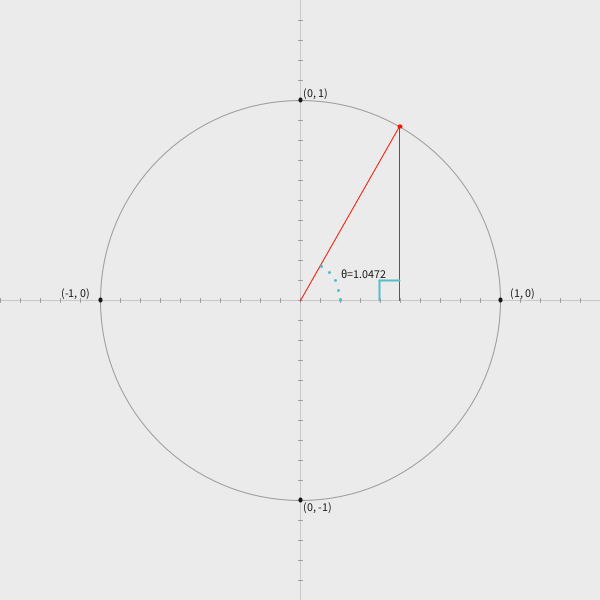
The challenge was to translate the Processing window coordinates into Cartesian coordinates, then create a graph of the unit circle.

Unit circle: implemented with Processing

size(600, 600);
textSize(12);
background(235);
noFill();

// translate to Cartesian plane for entire sketch
translate(width/2, height/2);
scale(1, -1);

stroke(200);
line(-width/2, 0, width/2, 0);
line(0, -height/2, 0, height/2);

for (int x = -width/2; x < width/2; x += 20) {
  if (x % 200 == 0 && x != 0) {
    stroke(100);
    line(x, 4, x, -4);
  } else {
    stroke(155);
    line(x, 2, x, -2);
  }
}

for (int y = -height/2; y < height/2; y += 20) {
  if (y % 200 == 0 && y != 0) {
    stroke(100);
    line(-4, y, 4, y);
  } else {
    stroke(155);
    line(-2, y, 2, y);
  }
}

/*
 * Translation from actual scale to unit-circle scale:
 * x = -1: -200
 * x = 1: 200
 * y = 1: 200
 * y = -1: -200
 *
 * Distance of 0.1 is 20px
 * */

// "unit" circle
ellipse(0, 0, 400, 400);

// points at each PI/2 angle
strokeWeight(4);
stroke(25);
point(200, 0);
point(0, 200);
point(-200, 0);
point(0, -200);

// an angle at 60 degrees
strokeWeight(1);
float radians60 = 60 * PI/180;
float x60 = cos(radians60);
float y60 = sin(radians60);
stroke(244, 23, 4);
line(0, 0, x60*200, y60*200);
line(x60*200, 0, x60*200, y60*200);

strokeWeight(4);
point(x60*200, y60*200);

// 90 degree angle indicator
stroke(86, 189, 199);
strokeWeight(2);
line(x60*200-20, 0, x60*200-20, 20);
line(x60*200-20, 20, x60*200, 20);


// dotted line to indicate the angle
strokeWeight(3);
stroke(86, 189, 199);
for (float theta = 0; theta < radians60; theta += 0.25) {
  float x = cos(theta) * 40;
  float y = sin(theta) * 40;
  point(x, y);
}

// flip the scale of y to prevent text from being written upside down
fill(25);
pushMatrix();
scale(1, -1);

// the y axis needs to be translated for each text y value
pushMatrix();
translate(0, -44);
String formattedRadians = String.format("%.4f", radians60);
text("θ="+formattedRadians, 41, 22);
popMatrix();

pushMatrix();
translate(0, -6);
text("(0, 1)", 210, 3);
text("(-1, 0)", -240, 3);
popMatrix();

pushMatrix();
translate(0, -406);
text("(0, 1)", 3, 203);
popMatrix();

pushMatrix();
translate(0, 420);
text("(0, -1)", 3, -210);
popMatrix();

popMatrix();

Translating the Processing coordinate system to a Cartesian plane

This is covered in notes / Using the Cartesian coordinate system in a Processing sketch. I confirmed that after translating the sketch’s coordinate system with:

translate(width/2, height/2);
scale(1, -1);  // flip the y-axis

calls to text() need to be made with a pushMatrix()/popMatrix() block. Within that block, a call to scale(1, -1) is made to prevent text from being rendered upside down. A call to translate(0, < -2 times the text y value >) is made to offset the effect of the call to scale(1, -1).

Formatting number strings with Java

Numbers rendered as strings can be truncated in Processing/Java with the String.format() method. To truncate a float’s decimal component, use the format ".4f" (with 4 or some other value following the . character.)

Finding an x or y value when the angle and either x or y is known

This wasn’t used in the final sketch, but for my own reference:

Say $\theta = 28^\circ$ and $x = 180$ . What’s the value of $y$ ?

Going back to SOH CAH TOA: $\tan(\theta) = \text{opposite}/180$ , $\text{opposite} = \tan(28^\circ)\cdot 180$

Start by converting $20^\circ$ to radians

28/360 = x/2\pi

x = 2\pi \cdot 28/360 = \pi \cdot 28/180 = 0.4886921905584123

Calculate $y$

y = tan(0.4886921905584123)\cdot 180 = 95.70769769906617

The above calculations were made with NumPy (64 bit precision(?)). The values calculated by Processing are similar:


size(600, 600);
textSize(12);
background(235);
noFill();

// translate to Cartesian plane for entire sketch
translate(width/2, height/2);
scale(1, -1);

stroke(200);
line(-width/2, 0, width/2, 0);
line(0, -height/2, 0, height/2);

for (int x = -width/2; x < width/2; x += 10) {
  if (x % 100 == 0 && x != 0) {
    stroke(100);
    line(x, 4, x, -4);
  } else {
    stroke(155);
    line(x, 2, x, -2);
  }
}

for (int y = -height/2; y < height/2; y += 20) {
  if (y % 100 == 0 && y != 0) {
    stroke(100);
    line(-4, y, 4, y);
  } else {
    stroke(155);
    line(-2, y, 2, y);
  }
}

float x = 180;
strokeWeight(4);
point(x, 0);

float angle = 28;
float angleRad = PI * angle/180;
println("28 degrees in radians: ", angleRad);

float y = tan(angleRad) * x;
println("y: ", y);

point(x, y);
line(0, 0, x, y);

Tags: