Malkus waterwheel (simulation)

A computer simulation of two Malkus waterwheels with different initial conditions. The initial angle $\theta$ differs between the wheels by 1 degree. The red and green lines are plotting the centers of mass of each wheel.

Plotting the waterwheel in 2 dimensions

Note that what follows is speculative (on my part).

The Malkus waterwheel is a 3 dimensional system. The waterwheel is a physical 2D object (in terms of it rotating on a plane), but its state is described by 3 variables:

• angular velolicy: how fast it’s spinning
• angular position: where it is in its rotation
• water distribution

The plots shown in the video are a 2D reduction of the system. This is done by plotting the trajectory of the center of mass of the wheel.

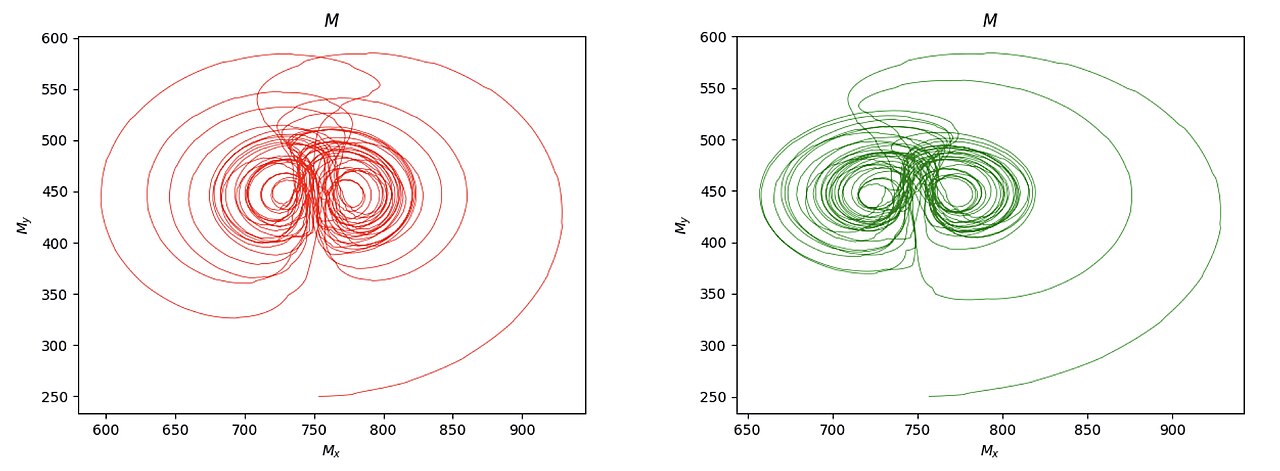
The center of mass is the vector $(\mathbb{M}_x, \mathbb{M}_y)^T$, where $\mathbb{M}_x$ and $\mathbb{M}_y$ are the $x$ and $y$ components.¹. The moving center of mass makes intuitive sense, but I don’t yet understand where $\mathbb{M}_x$ and $\mathbb{M}_y$ are coming from. I’m guessing the masses of the buckets on either side of the axis of rotation.

Related

• Malkus waterwheel (real)

References

Wikimedia Contributors. “Malkus waterwheel.” Accessed on: January 15, 2026. https://en.wikipedia.org/wiki/Malkus_waterwheel .